Programación dinámica es uno de los conceptos mas importantes en los últimos años dentro de la industria, pero ¿por que se volvió tan relevante y como apareció?
Por muy "rimbombante" que suene la verdad es que la programación dinámica no tiene en absoluto nada que ver con su nombre y esto es por que su creador Richard Bellman creo el concepto como un medio para conseguir fondos para poder seguir financiando su investigación matemática, así que utilizo un nombre tan "rimbombante" para sorprender a los congresistas y que no pudiesen negarle los fondos.
¿Y entonces que es la programación dinámica? Bueno pues en esencia es una forma de optimización de algoritmos, hace uso de varias técnicas pero lo mas importante es que la programación dinámica cambia tiempo por espacio ya veremos como es que pasa esto pero primero debemos saber que no todos los problemas pueden ser resueltos por programación dinámica, deben existir algunas condiciones para que pueda ser usada.
- Subestructura optima: Esto se refiere a que una solución global sea la suma de muchas soluciones locales.
- Problemas empalmados: Que consiste en resolver el mismo problema varias veces.
Estos son los conceptos y si notamos la subestructura optima parece que casi cualquier problema lo tiene, es decir en programación orientada a objetos tenemos clases y métodos que se van separando y haciéndose mas pequeñas de a cuerdo al nivel de abstracción que usemos pero no siempre tenemos problemas empalmados es decir estar haciendo varias veces lo mismo para llegar a una solución no ocurre todo el tiempo. Una vez conociendo las condiciones para que pueda existir la programación dinámica regresemos a eso de sacrificar tiempo por espacio.
- Memoizacion: Esto es mas que nada guardar el resultado de cálculos previos en una estructura, por lo general un diccionario y esto debido a que los diccionarios nos permiten realizar consultas con una complejidad de O(1) es decir la mas baja de las complejidades.
Muy bien ahora si vamos al ejemplo para ver como es que la programación dinámica es tan importante en problemas de optimización.
La sucesión de Fibonacci como ya deberíamos de saber tiene una solución recursiva Fn = Fn-1 + Fn-2 en Python es algo como esto:
python
def fibo(n):
if n == 0 or n == 1:
return 1
return fibo(n - 1) + fibo(n - 2)Esta es la solución recursiva pero vamos a ver su gran problema, ya que para nada es una solución eficiente.
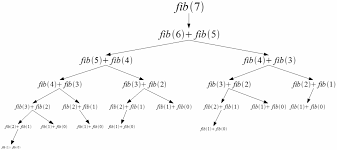
En la imagen podemos observar como hay una serie de cálculos que se repiten, por ejemplo el fibonacci de 4 se calcula 4 veces, incluso si tratamos de calcular el fibonacci de 50 nuestras computadoras tardarían varios minutos e incluso tal vez horas hasta obtener un resultado.
Ahora veamos la solución con programación dinámica.
def fibo(n, memo={}):
if n == 0 or n == 1:
return 1
try:
return memo[n]
except KeyError:
resultado = fibo(n-1, memo) + fibo(n-2, memo)
memo[n] = resultado
return resultadoEn esta solución lo que estamos haciendo es retornar el resultado de los valores que ya calculamos previamente ahorrándonos muchos recálculos. Y si corremos esto con fibonacci de 50 la solución es casi inmediata.
Sin embargo no todo es así de perfecto, ya que como dijimos sacrificamos tiempo por espacio, pero espacio que hasta el día de hoy es limitado así que debemos ser cuidadosos en cuando usamos esta técnica para resolver problemas.
Recuerda que tenemos un curso de fundamentos de python en donde podrán aprender mas sobre este lenguaje y si bien la programación dinámica no es exclusiva del lenguaje podrán entender mucho mas de ella en un lenguaje tan fácil de aprender como lo es python.

